OLBERS' PARADOX - THE SIMPLEST RESOLUTION (?)
OLBERS - THE PARADOX
Does the Universe go on for ever in space, or does it have an end, an outer edge? And does it go on for ever in past time, or did it have a beginning? These are pretty big questions, which have challenged and unsettled human thinkers since ancient times, so it is perhaps rather surprising that there is a very simple argument which goes some way to answering them and which depends only on a childishly simple ‘astronomical’ observation which can be made even when the sky is completely cloud-covered: it is dark at night. This argument, Olbers Paradox, was first precisely stated by the German astronomer Heinrich Olbers about 1820, although there are vague anticipations of it in the earlier writings of Kepler, Halley and others.
The argument starts from the simplest
possible set of assumptions: (1) the Universe, that is the
distribution of stars in space, is infinite; (2) those stars
have shone, just as now they shine, for ever – that is, the
Universe is eternal 1; (3) the rules of geometry
applicable to the Universe are those of Euclid; (4) Energy,
including that of starlight, can neither be created nor
destroyed – the Conservation of Energy, arguably the most
fundamental of all Nature’s laws.
1 These are big assumptions but they are, at least, one possibility logically and we have to start somewhere; the argument goes on to deduce a contradiction – The Paradox – from them, so proving that they cannot both be true. That is, Olbers’ argument is a reductio ad absurdum, a standard method in logic and mathematics for proving the contrary of what is assumed.
Now think of us standing on Earth and looking out
at the starry heavens beyond. From God’s view, the situation
would look like this:
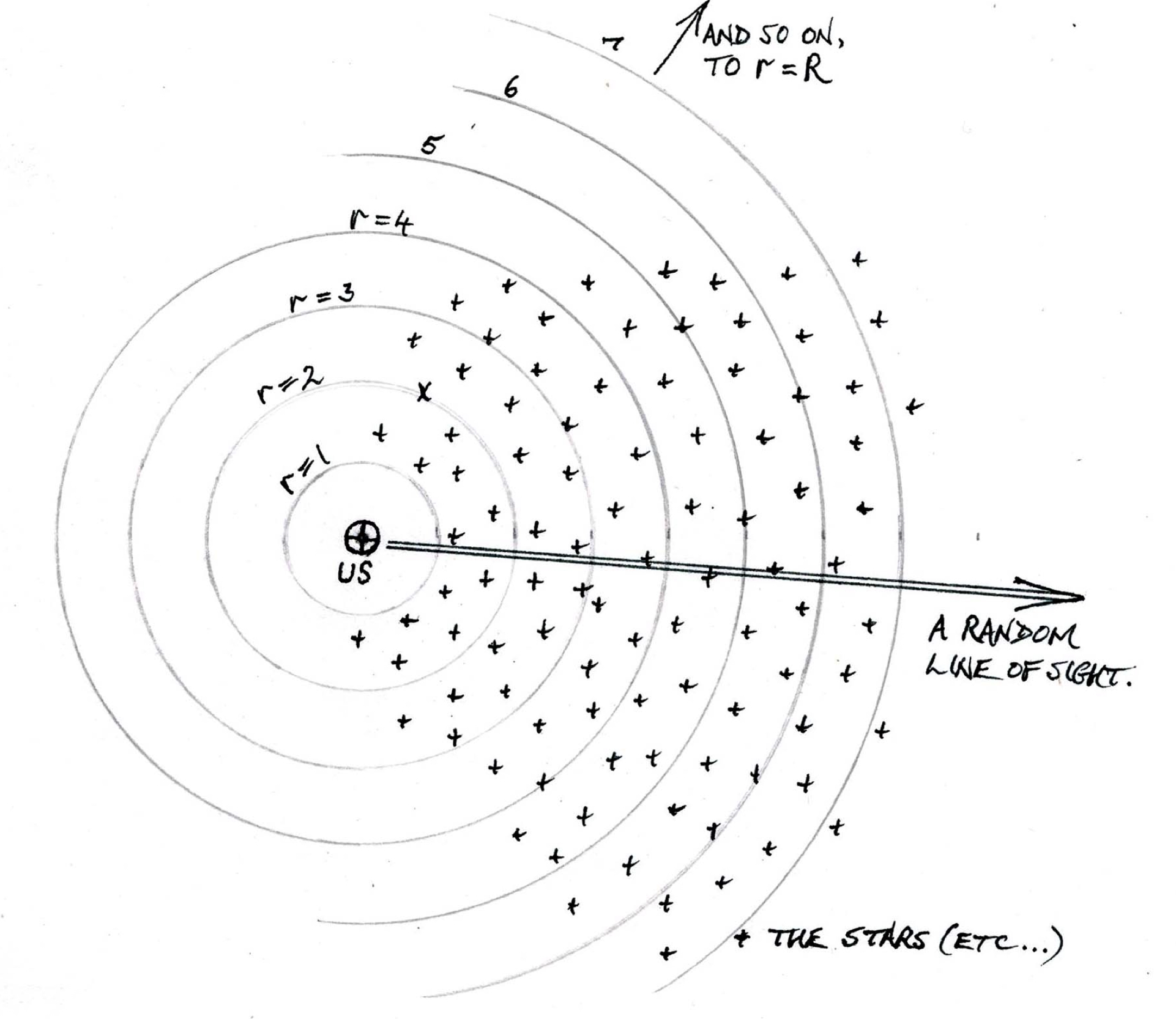
where for purposes of the argument the whole of space and the stars in it have been divided into concentric spherical shells of equal thickness centred on the Earth and so extending from radius r =1 to r = 2, from r = 2 to r = 3, and so on, out to some limit (maybe finite, maybe not) r = R. What the unit is for these radial measurements doesn’t matter, the argument will be exactly the same because the only question of interest about R is whether it is finite or not.
Now suppose that the stars are distributed
with broadly constant numbers n per unit volume of space
throughout the Universe 2 and that, on
average, they each have a cross-sectional (e.g. equatorial) area
A. Then there will be n stars each of such area A for each unit
surface area of each of
the spherical shells, precisely because each shell is of unit
thickness (think about it!). Provided that the ‘unit’
shell-thickness is taken small enough that there is no overlap
of stars within the shell as seen from Earth – and we are free
to take that unit whatever we please – each unit surface area of
the shell will then have an area nA of star-surface in
projection on the sphere and area (1-nA) of empty sky. The probability,
therefore, that a randomly-chosen line of sight from Earth will
pass through this shell without hitting the surface of a star is
= (1-nA)/1. Note that this probability (1-nA) does not depend on
the radius r and so is the same for all the shells.
Therefore the probability of that line of sight passing
right out through all
the R unit shells without ending on a star is P = (1-nA)R
, since the chance at each shell is completely independent of
those at all the other shells (independent trials, a ‘Binomial
Model’).
2 Another assumption, spatial homogeneity, but for the purposes of the argument it is only necessary to assume this in the very roughest average, on the most cosmic scale, transcending such trivial details as galaxies, clusters of galaxies and all those minutiae.
Now the crux of the matter: however small nA may be, and therefore however close (1-nA) is to 1, this probability P tends to zero as R tends to infinity: (1-nA)R→0 as R→∞ .
For numerical evidence of this, try (1-
0.0000001)R on your calculator for R=10, R=100,
R=1000, and so on…
The conclusion: In an
infinite globally-homogeneous universe (i.e. infinite R)
every line of sight ends on a star. That is, as seen
from Earth, the whole sky in such a universe would be
star-surface, with no dark sky between. A fairly
dramatic conclusion.
So far, only assumption (1) has been
explicitly invoked in the argument and the conclusion is already
looking pretty fishy. To avoid this, one might think of calling
in the finite speed, c, of light as a way out: if the Universe
was created a time T before the present, then no stars beyond R
= cT would yet be visible and it may be that cT is much smaller
than the R-value needed to fill the whole sky with star-surface.
3 This is where assumption (2) comes in – if
the Universe is eternal ; this ‘fix’ is not available,
every line of sight ends on a star and
its light will already be shining on us.
3 In fact, it is in our universe but that is only known in hindsight from a lot of specific results from modern observational astronomy, which is not the point here.
Taking one thing at a time, now invoke
assumption (3), that of cosmic geometry being Euclidean. In that
case, the surface area of any sphere drawn around a star
as centre increases as the square of its radius, so that on the
simple basis that light doesn’t just disappear in transit, and
that all the light coming out of the star must therefore cross
every such sphere, it follows that the intensity of the star’s
light must decrease inversely with the square of its distance.
This is the inverse-square law of photometry, a direct
consequence of Euclidean geometry and the non-vanishing of light
rays in transit. But the same Euclidean geometry also means that
the star’s angular apparent diameter decreases inversely as the
star’s distance and its apparent surface area, ∴, inversely as
the square of its distance. So the ratio:
star’s apparent brightness / star’s apparent area varies as (1/
distance squared)/ (1/ distance squared) and the result is that
the star-disk’s apparent surface-intensity is constant however
far away the star may be.
Finally, now
combining the two main conclusions above, it follows that in
an infinite, infinitely old universe, Euclidean in geometry
and globally homogeneous, the entire sky would be star-surface
completely undimmed by distance. It is truly remarkable that
the most general assumptions about the furthest reaches of the
Universe can produce a specific prediction so very easily
tested by an instant’s observation right down here on Earth 4.
And the prediction is spectacularly wrong – so at least one of
the original assumptions must be false: this is Olbers’
Paradox.
4 A classic case of the global directly affecting the local, of the macrocosm dictating to the microcosm. Another such is Mach’s Principle in dynamics, whereby the remotest matter in the Universe appears, somehow, to determine the local standard of non-rotation as revealed by Foucault pendulums, gyroscopes and your cup of tea (assuming you take sugar). It is probably fair to say that modern physics and cosmology has still not yet adequately taken account of the possible influence of such ‘cosmic feedback’ of the Universe as a whole on physics as studied locally in terrestrial laboratories. This, of course, would require a much more holistic view of the physical world than has generally been adopted by mainstream science.
What possible ways might there be of avoiding this incandescent-sky result? One might think that abandoning Euclidean geometry on the cosmic scale could be enough to do the trick. There are two difficulties with that idea. Firstly, it is far from trivially obvious that adopting any self-consistent non-Euclidean geometry would, even in principle, solve the difficulty. That question could only be settled by a careful and decidedly non-trivial mathematical investigation. Secondly, there’s not much point in pursuing that anyway because several missions mapping the Cosmic Microwave Background 5 (the ‘C.M.B.’) in great detail since about the turn of the present century have shown fairly conclusively that the geometry of the Universe ‘in the large’ is, after all, Euclidean. There are, indeed, cogent a priori reasons why the large-scale geometry must be ‘flat’ if there is to be any hope of explaining the creation – the creation of the Universe and everything in it – within the laws of nature as at present understood 6. In short, non-Euclidean geometry does not provide a likely let-out from the Olbers' Paradox.
5 The stratospheric balloon-borne Boomerang experiment, and the Earth-orbiting space observatories WMAP & Planck.
6 That intriguing issue may be discussed elsewhere in these notes on another equation.
One last
way out of the ‘difficulty’ might seem obvious: space is not
completely transparent but is filled with thin absorbing
material which blocks the light of very distant stars. This is
precisely what Olbers suggested in the 1820s. Such dark
interstellar material does indeed exist, as can be seen on any
clear night of late summer in the northern hemisphere, which
reveals the Milky Way through Cygnus and southwards to be
divided into two parallel ‘ways’ separated by a dark space, the
Cygnus Rift – huge clouds of cold dust between us and the more
distant parts of the galaxy.
However, as long
as the infinity assumptions (1) and (2) apply to the real
Universe this cannot work because of (4). In an infinite,
infinitely old universe of stars the Conservation of Energy
requires that any interstellar absorbing medium must itself be
heated by the starlight it absorbs until it re-radiates exactly
the same amount of light and heat that it blocks: as long as it
continues to absorb more than it re-radiates, its own internal
energy, and therefore its temperature, must continue to rise
which in turn means that it re-radiates ever more brightly. This
changing state of affairs continues until eventually a perfect
balance is struck between radiation absorbed and radiation
re-emitted, when and only when the absorbing material can
finally settle into a steady state of ‘local thermodynamic
equilibrium’ (‘L.T.E.’). Assumption (2) guarantees that the
Universe has an infinite length of time for this ‘eventually’ to
have happened long ago. So the energy principle (4) rules out
this way of avoiding the paradox.
Olbers himself was
writing about 25 years before the fully general conservation law
was established, at a time when the science of energy was not
fully understood, so his mistake is entirely understandable.
What is much less excusable is those far later writers, of which
there have been a number, who have continued to countenance the
completely fallacious ‘absorbing medium’ argument 7
: unless we are prepared to reject one of the most fundamental
laws of nature as currently understood, that argument is dead
and buried, and has been since 1850!
7
Extraordinarily, these have
included two of the greatest astronomers of the early 20th
century, Simon Newcomb on pages 73-4 of his undated but
circa 1906 Side-lights on Astronomy
and, early in his career, (later Sir) Arthur Eddington. In
his article ‘Star’ in the 11th edition of Encyclopaedia
Britannica 1911 vol. XXV,
p.792a, Eddington states the Paradox and then goes on to say
“…it is necessary however to emphasise that the
foregoing argument assumes that there is no appreciable
absorption of light in interstellar space. Recently, however,
the trend of astronomical opinion has been rather in favour of
the belief that diffused matter may exist through space in
sufficient quantity to cause appreciable absorption; so that
the argument has no longer the weight formerly attached to
it.” The striking irony here
is that it was precisely Eddington himself who only 5 years
later made the unavoidable requirement of radiative
equilibrium (aka L.T.E.) the basis for the theory of energy
transport in stellar interiors and hence that of stellar
structure, later expounded in his justly-famous book The
Internal Constitution of the Stars,
one of the great classics of 20th century astronomy! Strong
hints of the long-discredited ‘interstellar absorption’
argument stubbornly continue to surface in some popular
accounts of Olbers Paradox even now.
The final result of all of this is
therefore: if assumptions (1) and (2) were both true the sky
would be incandescent star-surface in all directions with no
dark sky between. This, plainly, is not true in the real world,
therefore those infinity-assumptions cannot both be true.
In fact, modern astronomical observations of the last 90 years in the remote depths beyond our galaxy have actually demonstrated exactly how (1) and (2) fail: Edwin Hubble’s discovery of the expansion of the Universe and its velocity-distance law in 1930 led to the realization that the whole thing began a finite time ago at a single point; Penzias and Wilson’s discovery of the Cosmic Microwave Background radiation in 1964-5 revealed the remnant flash from that explosive moment of creation, now hugely diluted and cooled by the subsequent Hubble expansion; and the Hubble Space Telescope’s ‘HDF’ or Hubble Deep Field of December 1995 showed unmistakeably that galaxies twelve billion (12 x 109 ) light years away, and therefore twelve billion years ago (‘look-back time’), were primitive, half-formed things quite different from present-day galaxies, so the HDF is direct pictorial evidence that the Universe is an ageing system which was still in its infancy 12 x 109 years ago.
These
discoveries, then, are unanimous in showing that T is finite and
that assumption (2) is false. Further, as they demonstrate that
the Universe began in a point-like superdense state a time T in
the past, and that it has been expanding at a finite rate over
that interval, its present spatial extent can only be finite too
and so assumption (1) is also false. So no Olbers inferno
arises.The three most important discoveries of 20th-century
cosmology can thus be quite legitimately seen as merely the
working out in detail of how exactly the real Universe avoids
the blazing fate envisaged by Olbers in 1820: Olbers' Paradox is
central to the understanding of modern scientific cosmology.
At the end of the argument set out above, it was the Conservation of Energy which finally proved that the assumptions (1) and (2) cannot both apply to the real world. Another very obvious way of seeing how energy considerations immediately demolish the eternity-assumption (2) is that, were it true, the stars would have to shine for an infinite length of time and each therefore produce an infinite amount of energy as starlight. Stars, however, are only finite bodies each containing, at most, only a finite amount of fuel (whatever that is), so again Conservation of Energy makes that impossible. In the separate manuscript notes of 5.xii.21 here the Universe’s maximum possible energy-budget is quantitatively estimated and shown to fall short by a factor of order 10,000 of that needed even to maintain starlight throughout all space at the level of everyday Earthly daylight. Even that large a level of cosmic illumination could only be attained if all the matter existing – worlds, star-systems and all – were transformed into the energy of starlight in one great blaze of annihilation: so much for the Olbers inferno!
Mathematical
afterthought:
In desperation,
one might think that ‘Olbers’ could be evaded by abandoning the
assumption of homogeneity, in which the star-density n was taken
to be constant on average throughout all space, and instead take
n = n(r) to be a steadily decreasing function of distance r from
Earth, so that the stars steadily thin out the further into
space we look. For instance, if n(r) = A/rk
,with the constants A & k both positive numbers, it is then
easily shown by an elementary exercise in integral calculus that
the total intensity of starlight is finite if and only if
k > 1, while the total number of stars in the universe is
itself finite if k > 3. So, in particular, n(r) = A/r² would
give a universe in which starlight on Earth was of finite
intensity even ‘though there is an infinity of stars – the
‘frayed-at-the-edges universe’, which might appear to be an
attractive way out of the paradox. This is not,
however, a viable way of evading ‘Olbers’: it requires the
distribution of stars to be spherically symmetric about our
particular vantage-point, i.e. it puts Earth at the centre of
the Universe, an infinitely improbable coincidence.
Exercise: verify these assertions by
integrating the star-density n(r) = A/rk
, and the intensity of starlight it produces, over spherical
shells of radius r (see earlier diagram) and thickness δr, from
r = a, the distance of the nearest star, to r = ∞.
A critique of the
argument above, and a shortcut to the same conclusion.
For anyone coming
to Olbers’ Paradox for the first time, it is just as well to
have the essential principles of its derivation set out as
separately and explicitly as has just been done. For the
sophisticate, however, who has already understood the full
inevitability of the Conservation of Energy implying the
interstellar-L.T.E. disproof of the ‘obscuring medium’ let-out,
there is a far slicker and quicker derivation, which also
disposes of the ‘non-Euclidean geometry’ let-out:
Whatever the global geometry may be,
let the surface area of a sphere be
A = A(r) : r ≥ 0 is its radius
– we make no assumptions about the form of A(r).
Then: (1) The number of stars
in each concentric shell of unit Δr is proportional to A(r);
And
(2) the light received from
each star on that shell is proportional to 1/A(r),
since, in the absence of light disappearing in transit (by
interstellar-L.T.E.), all rays leaving a star are spread out
uniformly over just such a spherical area by the time they are
received.
∴ the received light contributed by
each unit-Δr shell is ∝ A(r).1/A(r), which is constant and
positive whatever A(r) may be. Q.E.D!
Even this argument makes an assumption, however: that there are no one-way ‘energy sinks’ distributed throughout interstellar space. The reader may like to consider carefully why even distributing stellar- or planetary-mass black holes through all of space with just the right number-density would still not circumvent Olbers’ Paradox.
OLBERS'
PARADOX , THE SIMPLEST RESOLUTION (?)
